Действия с дробями. Задания ОГЭ

Прежде чем приступать к решению заданий с дробями, необходимо разобраться, что же такое дробь. Это можно сделать, прочитав статью “Как понимать дроби”. Будем надеяться, что с этим Вы уже разобрались. Теперь разберемся с основными действиями над дробями. Поехали.

№1 Сложение и вычитание дробей

В этом типе заданий могут встречаться как обыкновенные дроби, так и десятичные, а еще Вы можете встретить в одном примере сразу и такие, и такие.

Рассмотрим сложение обыкновенных дробей: $\frac{14}{25} + \frac{3}{2}$

Первым делом необходимо найти общий знаменатель этих двух дробей, для этого нужно перемножить знаменатели ~~те что снизу~~ между собой (25 и 2). То есть, общий знаменатель равен 50.
Затем нужно умножить числитель первой дроби на знаменатель второй дроби (14•2), а числитель второй дроби умножить на знаменатель первой дроби (3•25). Получается крест-накрест.
Теперь запишем общую дробь: $\frac{14\cdot 2 + 3\cdot 25}{25\cdot 2}$
Осталось выполнить умножение и сложение: $\frac{28 + 75}{50} = \frac{103}{50}$
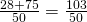
В таком виде ответ не получится написать в бланк, нужно привести полученную дробь к десятичному виду, то есть разделить в столбик 103 на 50. Получится 2,06.

При вычитании меняется только знак + на знак –

Например, $\frac{1}{5} - \frac{3}{4}$ .

Находим общий знаменатель (5•4 = 20).
Умножаем числитель первой дроби на знаменатель второй дроби (1•4 = 4), а числитель второй дроби – на знаменатель первой дроби (3•5 = 15).
Запишем общую дробь: $\frac{1\cdot 4 + 3\cdot 5}{5\cdot 4}$
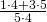
Выполнить умножение и вычитание: $\frac{4 - 15}{20} = \frac{-11}{20}$
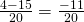
Разделим в столбик -11 на 20. Получится -0,55.

№2 Умножение и деление дробей

Умножение вообще происходит элементарно: перемножаем числители двух дробей и перемножаем знаменатели двух дробей. Например, $\frac{3}{5} \cdot \frac{3}{4} = \frac{3 \cdot 3}{5 \cdot 4} = \frac{9}{20}$ . Приведем к десятичной дроби = 0,45.

Деление отличается от умножения лишь тем, что вторая дробь переворачивается (числитель и знаменатель меняются местами). Например, $\frac{2}{3} : \frac{5}{6} =\frac{2}{3} \cdot \frac{6}{5} = \frac{2 \cdot 6}{3 \cdot 5} = \frac{12}{15}$ = 0,9

№3 Возведение дроби в степень

Рассмотрим такой пример: $(\frac{1}{5})^2$ . Дробь необходимо возвести в квадрат. Подробнее о возведении в степень можно узнать в статье “Что такое возведение в степень”. Отличие дроби от целого числа состоит только в том, что у нее есть числитель и знаменатель, и чтобы возвести ее в степень, нужно отдельно возвести в степень и числитель и знаменатель. В нашем случае дробь перепишется в виде: $\frac{1^2}{5^2}$ . А далее возводим числитель и знаменатель в квадрат: 1² = 1•1 = 1; 5² = 5•5 = 25. Получим, $\frac{1^2}{5^2} = \frac{1}{25}$

Видите, как все просто.

№4 Сложение/вычитание и умножение/деление дроби и числа

Все Вы встречали такие примеры: 3 + $\frac{3}{2}$ , 8 • $\frac{1}{8}$ и т д. Что же делать? Как это решать? Да так же как и обычно, только в этом случае целое число нужно переписать в виде дроби. В школе учат, если число умножить на единицу, то в этом случае единица не пишется (5•1 = 5). Логично! Таким образом любое целое число можно записать как это число, умноженное на единицу (5 = 1•5). То же самое и с делением! 3 = $\frac{3}{1}$ , а также наоборот $\frac{3}{1}$ = 3.

Решим первый пример: 3 + $\frac{3}{2}$ = $\frac{3}{1} + \frac{3}{2}$ . Приводим к общему знаменателю (1•2 = 2), и умножаем числитель первой дроби на 2, а числитель второй дроби на 1. $\frac{3 \cdot 2 + 3 \cdot 1}{2} = \frac{6+3}{2} = \frac{9}{2}$ = 4,5. При вычитании меняем только знак на минус.

Решим пример с умножением: 8 • $\frac{1}{8} = \frac{8}{1}\cdot\frac{1}{8} = \frac{8 \cdot 1}{1 \cdot 8} = \frac{8}{8}$ = 1.

Вот мы и познакомились с основными действиями над дробями. Далее рассмотрим решение конкретных заданий с дробями.